Why Is F/16 Smaller Than F/2? What Role Does Pi Play? And What’s Up With F/Stops, Anyway?
An aperture set at f/2 is twice as big as one set at f/2.8 and four times larger than f/4. What’s Pi got to do with f/stops, and why do we use such a seemingly arbitrary numbering system? Continue reading to learn the answers to these and a few more arcane aperture facts.
Exposure is controlled by adjusting the aperture of the lens and speed of the camera’s shutter. We all know this. If this is new to you, think of the aperture as a window and the shutter speed as the amount of time that window is held open.
The effect shutter speeds have on exposure is pretty easy to understand. 1/100 of a second is obviously half as long as 1/50 of a second. Reducing exposure by half is as easy as dialing in a shutter speed that’s half as long, provided the aperture remains the same.
But f/stops are like armadillos—even after looking at them 100 times, the way they’re put together sort of makes sense, but not much.
Part of the problem stems from the fact that an f/stop is a fraction. It’s the ratio between the lens’s focal length and the diameter of the active aperture. For example, a 50mm lens that is set at f/2 has an aperture that is 25mm in diameter. Similarly, a 50mm lens that is set at an aperture that is 8.9mm in diameter is said to be set at f/5.6. Divide 50 by 8.9 and the quotient is (about) 5.6.
Remember high school algebra? Or was it geometry? Anyway, to calculate the area of a circle one multiplies the radius times the radius times Pi. Or in other words, the radius squared multiplied by the constant 3.14159.
If you’re still with me, look at the following table.
For a 50mm lens,
f/stop Diameter Radius Area of aperture
f/2 25.0 12.5 490.9
50/2 = f2 = 25mm /2 = 12.5mm
(12.5)(12.5)(3.14159)=490.9
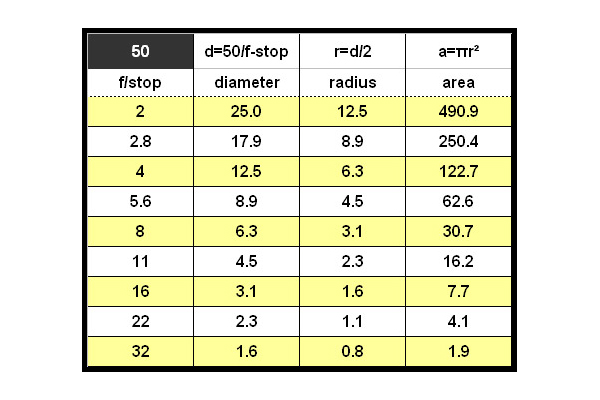 So, it’s (fairly) easy to see why f/2 is about twice as large as f/2.8. The area is about twice as large. As we go down the scale, each increment of one full f/stop equals a 2X change in exposure because the area becomes half as large. That is to say, each subsequent f/stop is one-half as large as the preceding f/stop.
So, it’s (fairly) easy to see why f/2 is about twice as large as f/2.8. The area is about twice as large. As we go down the scale, each increment of one full f/stop equals a 2X change in exposure because the area becomes half as large. That is to say, each subsequent f/stop is one-half as large as the preceding f/stop.
Why use such an armadillo-like system? Because it can be applied universally to all lenses of any focal length. For the purposes of calculating exposure, a 135mm lens set at f/5.6 delivers exactly the same amount of light as a 300mm lens at f/5.6. Were it not so, it would be virtually impossible to determine camera exposure settings by using an external handheld light meter.
The f/stop you select has dramatic impact on depth-of-field. We’ll save that topic for another day.
Incidentally, March 14, or 3.14 is Pi Day. Many schools—mostly elementary and middle schools—celebrate Pi Day with mathematics competitions. If you have a math teacher for a friend, share this story with them. Perhaps they can show their students that contrary to popular opinion, the junk they’re learning in class does have relevancy later in real life.
—Jon Sienkiewicz
- Log in or register to post comments